Меню
Вхід і реєстрація
Підручники нерідко і досі просто переповнені складною теорією та не надто цікавими завданнями. Утім, математика, це не лише лік і цифри, це ще і просторове мислення, логіка та прикладна математика. І для їхнього розвитку класичних рівнянь недостатньо, потрібні специфічні вправи. Саме тому наурок створили добірку цікпвих вправ, що продемонструють гнучкий підхід до завдань та сприятимуть багатогранному розвитку математичних навичок школярів.
Субітизація (від латинського «subitus» – раптовий) – функція сприйняття, що забезпечує миттєве визначення кількості предметів у полі зору, якщо ця кількість складає від одного до чотирьох (діапазон субітизації). Тобто у випадках, коли нам доводиться порахувати від одного до чотирьох об’єктів, оцінка їхньої чисельності відбувається миттєво і точно. А от якщо об’єктів більше, то час оцінки збільшується.
Пропонована гра працює саме за цим принципом, адже дитина має швидко оцінити кількість цяток у квадраті та об’єднати квадрати з однаковою їх кількістю. Якщо учні успішно впораються з цим завданням, можна ускладнити вправу, запропонувавши зіграти у гру, що є аналогом хрестиків-нуликів.
На полі №2 двоє дітей мають відшукати два квадрати з однаковою кількістю цяток та замалювати їх кожен своїм кольором. Як тільки один з гравців створює лінію з 3х квадратів, він виграє, тож завдання партнера – не лише провести лінію, але і перекрити супернику можливість утворити свою.
У цю гру можна грати самостійно. Попросіть дітей відшукати три квадрати з однаковою кількістю цяток та поєднати їх прямою або ламаною лінією. Таке завдання чудово тренує швидкість візуального сприйняття та оцінку кількості предметів.


Багато хто з дітей має непогані навички лічби, але при цьому не дуже добре справляється з завданнями на орієнтування у просторі. Тоді як ці вміння дійсно важливі та стануть у пригоді під час прогулянок містом, а згодом – у проєктуванні чи кермуванні авто.
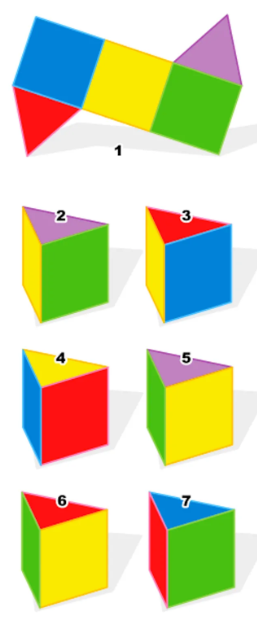
Для розвитку ментального проєктування використовуйте комплекс вправ, що вимагають скласти в уяві розгорнутий кубик та співставити, де знаходитимуться його сторони. Запропонована нижче головоломка має кілька варіантів рішення. Правильними будуть відповіді під номерами 2, 3 і 6, що відображають грані призми під різними кутами погляду.
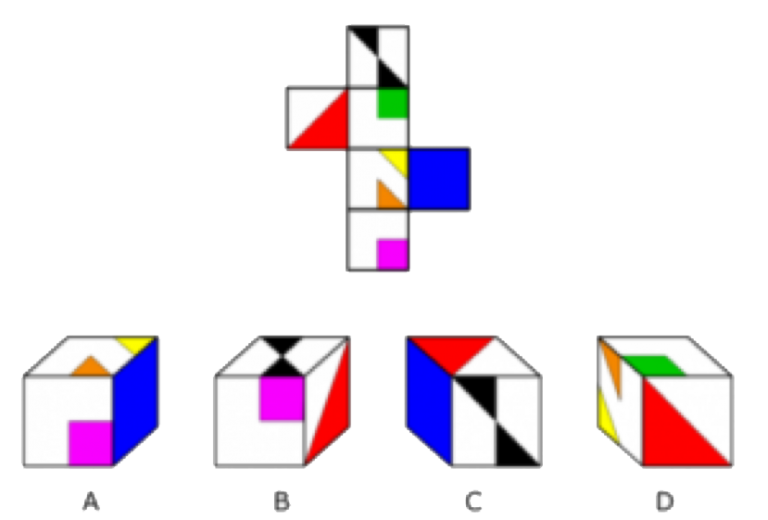
Правильна відповідь для вправи нижче – А.
Правильна відповідь для вправи нижче – знову А.

Наступний комплекс вправ схожий на попередній, але тепер необхідно настільки детально уявити предмет, щоб визначити напрямок його руху. Запитайте дітей – як мала рухатися фігура «А» аби змінити розташування так, як вказано на другому малюнку? Отже, дитині необхідно уявити траєкторію руху та намалювати її кольоровим олівцем поверх малюнка.
Малюнок №1.
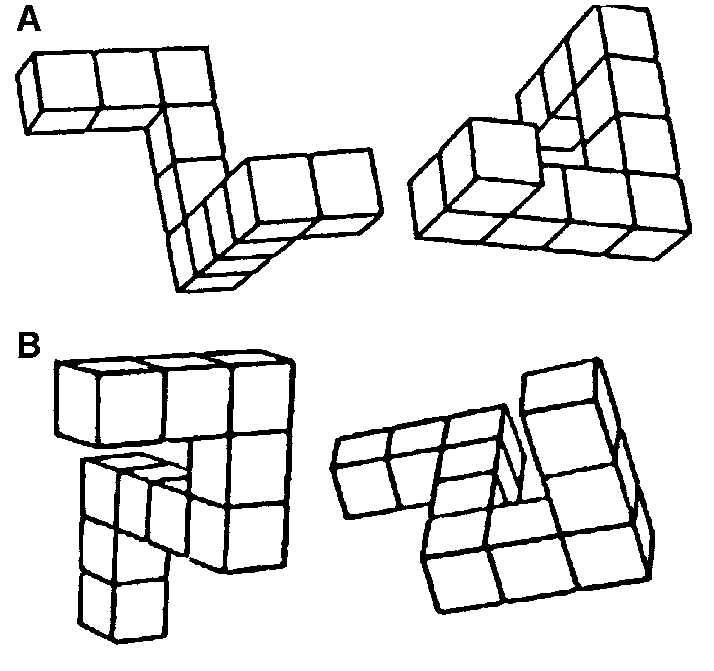
Інший приклад – обертання об’єкту, де необхідно виявити, яка з запропонованих фігур відповідає формі основного предмета (малюнок №4).
Малюнок №2.
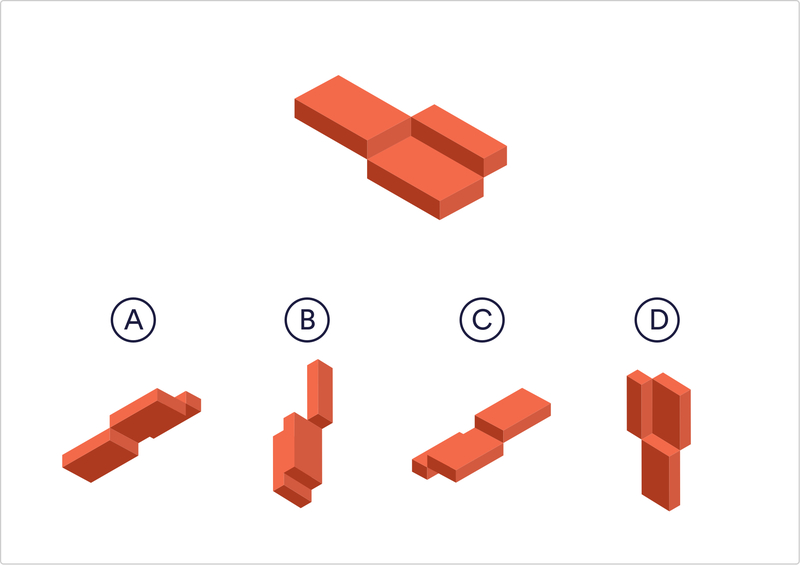
Малюнок №3.
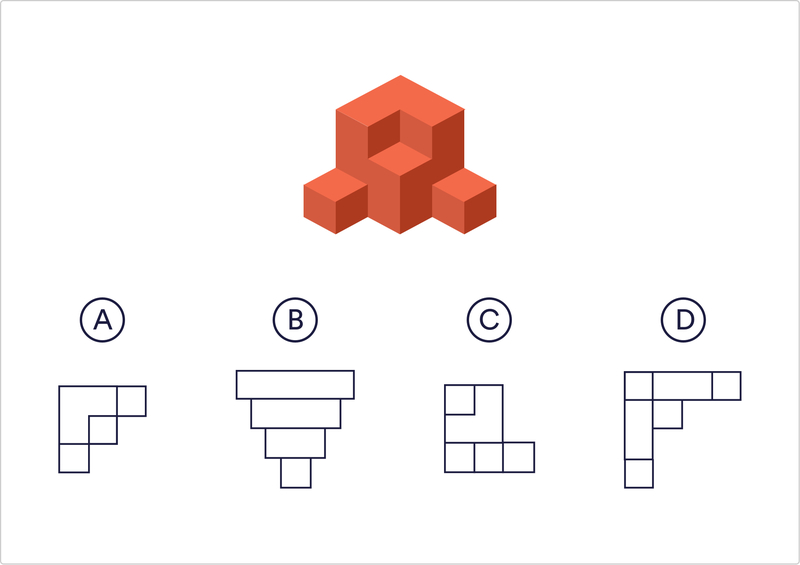
Малюнок №4

У наступних вправах необхідно співставити числа з фігурами та визначити, яка цифра відповідає кожній із них. Отже, щоб вирішити рівняння, маємо визначити складові суми.


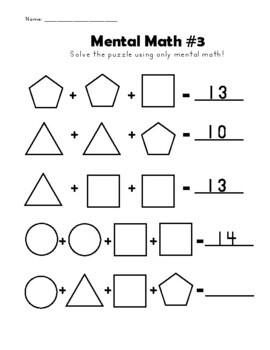

Вправи на виявлення логіки послідовностей.

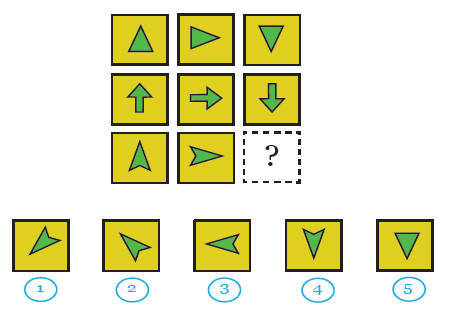
Дітям відомо, що математика може значно спростити життя. А як щодо виграшу у лотерею чи певного роду ігор, де перемога залежить від чистої випадковості? Утім, чи бувають у світі випадковості? Можливо, математика допоможе і тут?
Красномовну відповідь на це запитання дає наступна вправа – парадокс Монті Хол. Вперше це завдання отримали учасники телешоу, де ведучий пропонував обрати одну з трьох дверей. За однією знаходилася машина, тоді як за двома іншими – звичайнісінька коза. Аби отримати машину, гравець мав вгадати правильні двері. Шанс с на перемогу був – 1 із 3.
Наступний хід ведучого зробив це шоу значно цікавішим та приніс йому всесвітню популярність. Коли гравець обирає двері, наприклад – №1, Монті відкриває одну з двох інших дверей. При цьому він завжди обирає ту, за якою знаходиться коза – умовно, №2. Після цього він запитує у гравця – чи не бажає той змінити своє рішення, відмовившися від дверей №1 і обрати замість них №3?
Запитайте клас – як би вчинили вони? Імовірно, багато хто з дітей забажає лишитися зі своїм нинішнім вибором – двері №1, адже не бачать сенсу обирати нову ціль. Шанс виграти здається однаковим – 50 на 50. Якщо відповідь дітей буде саме такою, то вони помиляються.
Річ у тім, що з точки зору математики первинний шанс для дверей №1 бути виграшними – від 1 до 3 (33%). Утім, після того, як ведучий демонструє, де ховається коза, шанс для №3, стає вдвічі більшим – 2 з 3 (66%). Отже, змінивши рішення, ви збільшуєте свої шанси на виграш. Звісно, це не гарантує перемоги, втім, якщо грати у гру постійно, то згодом завдяки такій стратегії ви виграватимете частіше, ніж якби відстоювали первинний вибір.
Аби довести дітям правильність математичної моделі, об’єднайте клас у дві групи. Нехай перша група дітей завжди лишається зі своїм першим вибором, а друга завжди перемикається. Через кілька ігор ви почнете помічати, що другій групі таланить значно частіше.
Як бачимо, нетипові математичні вправи здатні не лише розвинути логіку, але і продемонструвати можливості науки, що подекуди нагадують магію або передбачення. Використовуйте ці вправи аби розвинути креативне мислення дітей, адже вони примушують працювати як ліву, так і праву півкулі мозку, що робить підхід до вирішення проблем більш гнучким.
Приєднуйтесь до нашої сторінки і групи у Фейсбуці, спільнот у Viber та Telegram
Теги: вчителям , логіка , математика , нестандартне мислення , освіта в Україні , поради
Приєднуйтесь до нашої сторінки у Facebook
«Освіта Нова» — у вашій стрічці новин